Goodness of Fit in MDS and t-SNE with Shepard Diagrams
The goodness of fit for data reduction techniques such as MDS and t-SNE can be easily assessed with Shepard diagrams. A Shepard diagram compares how far apart your data points are before and after you transform them (ie: goodness-of-fit) as a scatter plot. Shepard diagrams can be used for data reduction techniques like principal components analysis (PCA), multidimensional scaling (MDS), or t-SNE.
Plot Goodness of Fit with a Shepard Diagram
In this post, I illustrate goodness of fit with Shepard diagrams using a simple example that maps the locations of cities in Europe using t-SNE and MDS. You will see that the t-SNE approach, which is not designed to preserve all distances in the data, produces an odd-looking map of Europe and a distorted Shepard diagram. While the MDS approach produces an ideal-looking Shepard diagram. This is because MDS does not introduce any distortions in data which has only two dimensions. I then look at real (high dimensional) data using t-SNE and MDS Shepard diagrams.
The t-SNE example
I'll start with an example of t-SNE. The chart below uses t-SNE to place European cities on a map using a matrix of distances between cities of Europe. Having previously championed t-SNE, something has clearly gone wrong on this map.
First and most obvious, the orientation of the map is incorrect. It is rotated roughly 90 degrees clockwise. More northern cities are on the right of the map. In fact, this is not a failure of t-SNE. The algorithm doesn't know that conventionally we put north at the top, so we are free to rotate the output.
More seriously, the relative distances and placements on the map are wrong. For example, in reality, Madrid is significantly further away from London than Copenhagen is. I described in an earlier post why this happens: t-SNE tries to maintain the placement of each point amongst its closest neighbors. So it does not aim to get the distances correct.
This is a trivial example because we know how the true map should look. If we didn't know where the cities of Europe really are, how could we tell if t-SNE produced an accurate visualization?
Using a Shepard Diagram for t-SNE
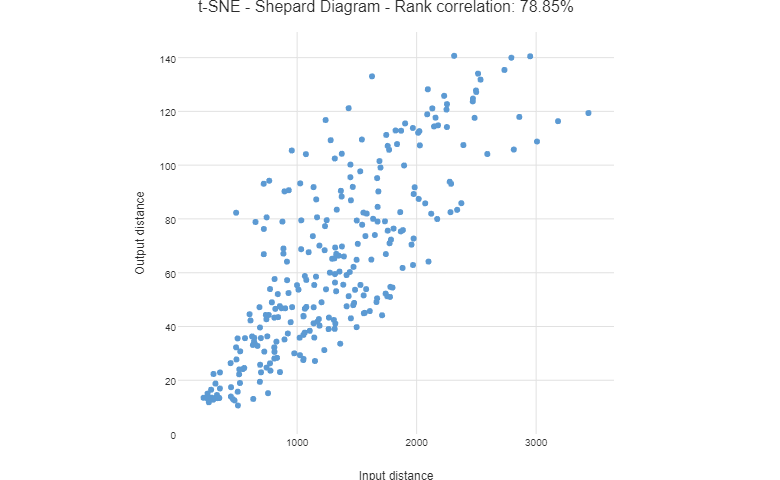
A Shepard diagram is one way of assessing if t-SNE produced an accurate visualization. It is a scatterplot of distances between data points. On the x-axis, we plot the original distances. On the y-axis, we plot the distances output by a dimension reduction algorithm. Below I show a Shepard diagram for t-SNE applied the map of European cities.
The scatter plot shows a rough correlation in that cities closer together in input space tend to be closer together in output space. However, by hovering over the points we can see that, for example, Brussels and Hamburg are too far apart. The fact that the Spearman's rank correlation is only 89% shows that the ordering of the distances is wrong in some cases.
Plot Goodness of Fit with a Shepard Diagram
Using Shepard Diagrams with Multidimensional Scaling (MDS)
Whilst t-SNE preserves local neighbors, MDS takes a different approach to mapping. It has 2 main variants:
- Metric MDS minimizes the difference between distances in input and output spaces.
- Non-metric MDS aims to preserve the ranking of distances between input and output spaces.
Applying metric MDS to the European cities gives the map below. You might recognize this as being correct (if you rotate it around a little).
Because we start with a distance matrix derived from 2 dimensions, MDS is capable of faithfully recreating the map. In other words, there is no information loss. This is true of both the metric and non-metric versions. We can confirm the accuracy from the Shepard diagram below. This shows that the mapped distances are in the same order as the original distances.
Plot Goodness of Fit with a Shepard Diagram
While a really accurate dimension reduction like the one above will produce a straight line. However since information is almost always lost during data reduction, at least on real, high-dimension data, Shepard diagrams rarely look this straight.
Applying t-SNE and MDS to High Dimension Data
Let's try and apply the techniques above on a real data set. In a previous analysis, I used t-SNE to reduce the dimensionality of a data set which described the physical characteristics of leaves from a variety of plants. The Shepard diagram for the t-SNE analysis reveals a rank correlation of 86%.
Metric MDS produces the following chart for the leaf dataset.
The MDS groups species more loosely than the t-SNE. So the rank correlation from the Shepard diagram is 90%, which is slightly better than the t-SNE.
Non-metric MDS aims to maintain the distance ranking. So it is no surprise that it has an even higher rank correlation of 97% as shown below.
t-SNE versus MDS: which is better?
Which method is better? That depends on what we mean by "better". t-SNE's strength lies in creating tight clusters for visualization. Often we care more about relative positioning than absolute differences, in which case non-metric is preferred to metric MDS.
Software for Shepard diagrams
In Displayr, PCA, t-SNE, and MDS options are all available under Insert > More > Dimension Reduction. You can create a Shepard diagram by selecting Insert > More > Dimension Reduction > Diagnostic > Goodness of Fit Plot. Select your PCA, t-SNE, or MDS in the Dimension Reduction menu under Properties.
In R, these Shepard diagrams are available using the GoodnessOfFitPlot() function from the flipDimensionReduction package.
Plot Goodness of Fit with a Shepard Diagram
Replicate this analysis
All the analysis in this post was conducted using R in Displayr. You can review the underlying data and code used in my analysis and create your own Shepard diagram analysis here. The flipDimensionReduction package (available on GitHub) was used, which itself uses the Rtsne and MASS packages.