How To Improve Data Visualizations Using Redundancy
Using multiple visual elements to represent one variable in a chart can increase accuracy and improve readability. This is called adding redundancy or redundant encoding and, if done right, it will improve the chances of a reader interpreting a visualization quickly and correctly. Redundant elements can be color, shape, size, labels, and more.
In the first section of this post, I show how adding redundancy to the same chart improves its readability. In the remainder of the post, I explain the theoretical underpinning of redundancy and use it to draw some less obvious conclusions about how to create and evaluate visualizations.
How adding redundancy improves readability
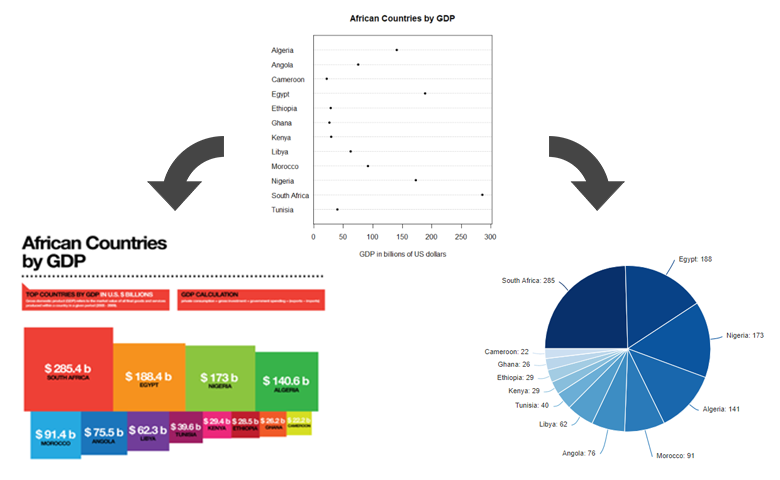
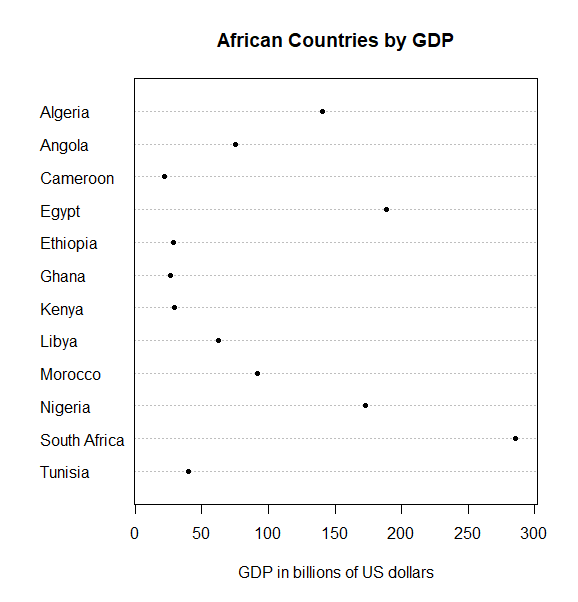
First, let us start with one of the most spartan of charts, the dot chart/plot. If you have ever read any of the work of William Cleveland, there is a good chance you will have a fondness for dot charts. They are simple and elegant. The plot below is the default dot chart in R. It shows the GDP for a range of countries using the horizontal position of each dot. The interpretation can easily be improved.
Adding redundancy by ordering the chart
The next version of this chart (below) was created by Andrew Gelman. Andrew did not suggest it was a perfect chart, so please do not interpret this post as any criticism of my favorite blogger. The difference is that the countries have been ordered according to their GDP.
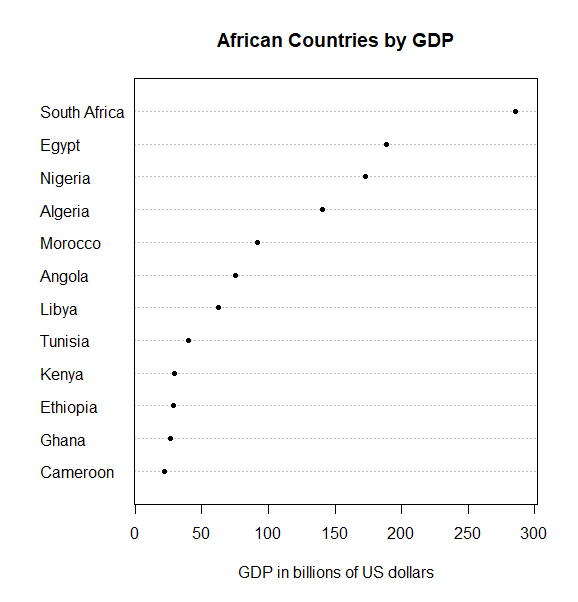
As you can see, ordering the countries by GDP improves the chart. This is a well-accepted principle. But, think for a moment. Why should re-ordering it make a difference? There are a number of reasons. The reason that I am focusing on in this post is that ordering the chart causes key results to be encoded twice. This reduces the expected errors in misinterpretation. Other reasons why this ordering is preferable relate to the speed with which we can decode the information.
Sorting a chart gives the viewer an additional way to read it. In the alphabetically-ordered chart, the user can only get insights by comparing individual points. In the sorted chart, the reader can also gain conclusions just by looking at the order of the categories.
Why should this make a difference? When we inspect a chart we are using our perceptual skills to make measurements. We run the risk of making mistakes. By encoding the chart with data in two different ways, the user has two chances to derive the conclusion. So long as the biases in each encoding are offset by the reduction in error caused by having two encodings, the quality of the visualization improves.
Changing to a bar chart adds two more redundancies
If we replace the dot chart with the bar chart we get a simple win. In one formatting decision, we add two additional encodings of the data. While the original dot plot encoded the data based only on the horizontal position of the dots, the viewer now has four ways to interpret the visualization:
- The right-most point of each bar (which is equivalent to the position of the dots).
- The width of each bar.
- The area of each bar.
- The order of the bars.
You may be reading this thinking "hold on, the right-most point, the width, and the area are all the same thing". Yes and No. Yes, they are all the same quantitative information. And, yes, they are not independent. But no, they are not perceptually equivalent.
Increasing the redundancy by adding value labels

We can increase the redundancy by adding labels that contain the values of each bar. This reduces perceptual errors in multiple ways. First, via redundancy. Second, it is easier, faster, and likely more accurate to read the value of 285 next to South Africa than to try and read it off an axis. Third, if we are lucky, we can further improve the visualization by moving the labels into the bars, thereby reducing the distortion effect that the category and value labels have on our ability to perceive bar length. I have illustrated this for the first four countries, but there is no neat way to do this for the remaining countries with this data set.
Adding redundancy by shading
Now for a more controversial change. I've shaded all the bars from highest to lowest. I have gone the lazy approach of shading them by order, but perhaps it would be a bit better to shade them more heat-map style in direct proportion to the values. This achieves yet another form of redundancy. Compared to the original dot plot which only encoded the data once, we are now encoding it six times: the horizontal position of the bar ends, the order of the categories, the width of the bars, the area of the bars, the value labels, and the shading.
Unlike all the previous additional forms of redundancy, shading is not without cost. Most obviously, people are poor at correctly inferring numeric values from shading. Less obviously, the shading increases the error of some of the other forms of information. In addition to the difficulty we now have in reading the values of the small countries, we have introduced a new and misleading visual cue: blueness.
Compare South Africa to Egypt in the above. When they had the same color, we could say that the ratio of the amount of blue (color * area) between South Africa and Egypt was 285 / 188. Now that we have changed the shading, the amount of blue is misleading. Is this additional form of redundancy worthwhile? I suppose that one could conduct a study. But to my mind the distortion is marginal and I think it looks nice, so I would choose to use it with this data.
Redundancy is a broadly applicable principle (it is not just about bar charts)
Consider the numbers below. The pattern is communicated in three ways: by the numbers, by the ordering, and by the decision to represent decimals without a 0. I have written .1 rather than 0.1. The reason for doing this is that it makes it so that the number of characters used for displaying each of the numbers is correlated with their values. (I first came across this idea in the writings of Andrew Ehrenberg, who was to tables what Tukey was to charts).
100.0 Big 10.0 Moderate 1.0 Small .1 Very small .0 Invisible
Compare the two pie charts below. While everybody hates the first one, the second one is only half-bad. The first pie chart has two encodings. These are the values in the labels and the sizes of the slices. The second pie chart is better because it adds two more encodings. It orders the slices from largest to smallest, and it shades the slices in the same way. And yes, before you write a comment, I know that both pie charts are misleading, as there are many more countries in Africa.
Using redundancy to evaluate the quality of visualizations
The effectiveness of redundancy at improving a visualization depends on the number of encodings, the quality of each encoding, and the relationships between the errors with each encoding. (If you are not familiar with these ideas, a good place to start is the Spearman-Brown prophecy formula, which explains why, for example, IQ tests ask lots of questions rather than just a couple. For a more in-depth explanation, checkout Psychometric Theory for what is, or at least was when I was young, the classic text).
As mentioned, the example in this post, which is reproduced below, is from a post by Andrew Gelman. It contains two encodings: order and the horizontal position.

Gelman contrasts the dot chart with the visualization below. Gelman makes the point that the visualization below is more arresting than his sorted dot chart, but the dot chart is better from something that he refers to as a "statistical graphic perspective".

This visualization has at least three encodings:
- The area of the squares (and perhaps also their heights, widths, and if we want to be a bit foolish, other size properties).
- The value labels.
- The order of the squares.
So, on a simple crude count, it is superior.
However, at least two of these encodings are worse than those used in the dot chart. The dot chart used a highest to lowest encoding or order, whereas the visualization uses a two-line left-to-right encoding. The latter is less transparent, less culturally-general, and thus less effective. Second, area as an encoding has long been known to be inferior to horizontal position. Furthermore, the visualization achieves a bit of its visual appeal by introducing an irrelevant coding, color. This can only serve to reduce the accuracy with which the visualization is decoded, all else being equal.
While I am sure it would be possible for somebody who had a lot of time on their hands to conduct an experiment working out whether the dot chart's two encodings lead to less error than the three encodings of the chart above, my guess is it is marginal. As the second chart is more arresting, it is probably the better visualization. Note though that the principle of redundancy provides a statistical framework for evaluating and comparing visualizations.
I have reproduced my final bar chart. As mentioned, it has six encodings. To my mind, it unambiguously dominates the dot chart. Is it better than the squares above? It is hard to know. However, if we could find a way to make it arresting without sacrificing the number and quality of the data encoding, we would be well ahead.
What is not a recommended type of redundancy in a visualization?
Not all redundancy is helpful—some can mislead or overwhelm. A key example is using color to encode quantitative data when viewers are unlikely to interpret it accurately. As discussed earlier with the shaded bar chart, while color can make a visualization more visually appealing or intuitive, it often introduces perceptual distortions. Our brains aren’t great at interpreting gradients or distinguishing subtle color differences, especially across a spectrum.
Redundancy also becomes problematic when encodings are not independent or when they interfere with one another—such as combining area and color in a pie chart, which can create a compounding distortion. Worse still is when redundancy distracts from the message, like decorative images, 3D effects, or inconsistent visual cues that compete for attention rather than clarify. In short, redundancy should reinforce understanding, not introduce confusion. If a redundant encoding doesn't improve speed, accuracy, or clarity, it's better left out.
Explore the R code
I have created all these examples using R. You can sign-in to the Displayr document that contains all the R code here. To see the code, click on any of the tables or charts, and select Properties > R CODE to the right. The R code will appear a bit messy for the pie charts, as I have hooked them up to controls on the Inputs tab.