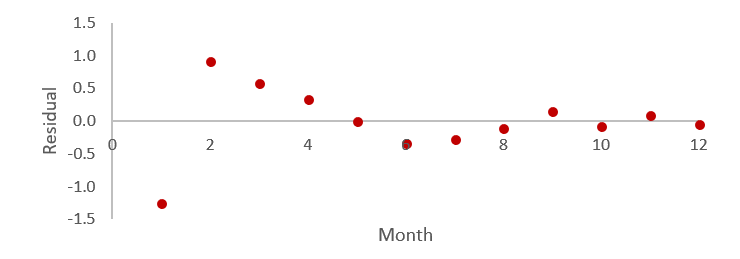
Heteroscedasticity (also spelled “heteroskedasticity”) refers to a specific type of pattern in the residuals of a model, whereby for some subsets of the residuals the amount of variability is consistently larger than for others. It is also known as non-constant variance.
Heteroscedasticity can be seen in the plot below, where the first four residuals have an average absolute value of 0.77, compared to only 0.13 for the remaining eight observations. That is, the first four observations are on average further from the 0-line than the remaining observations.
How to detect heteroscedasticity
When performing simple models -- those with only a single predictor, or time-series data -- you can diagnose heteroscedasticity using plots like the one above. However, with more complicated models you can typically only diagnose it using statistical tests.
The most widely used test for heteroscedasticity is the Breusch-Pagan test. This test uses multiple linear regression, where the outcome variable is the squared residuals. The predictors are the same predictor variable as used in the original model.
What are the implications?
When heteroscedasticity is detected in the residuals from a model, it suggests that the model is misspecified (i.e., in some sense wrong). Possible causes of heteroscedasticity include:
- Incorrectly assuming linear relationships in models
- Incorrect distributional assumptions (e.g., using linear regression when Poisson regression would be appropriate)
- Models that perform better for some subgroups than others (e.g., a model that performs well for women but poorly for men will exhibit heteroscedasticity)
The existence of autocorrelation means that the standard computations of standard errors, and consequently p-values, are misleading.
Fixes for heteroscedasticity
The best solution for heteroscedasticity is to modify the model so that the problem disappears. For example:
- Transform some of the numeric variables by taking their natural logarithms
- Transform numeric predictor variables
- Build separate models for different subgroups
- Use models that explicitly model the difference in the variance (as opposed to just modeling the mean, which is what most models do)
A simpler approach is to use robust methods for computing standard errors, such as Huber-White sandwich estimator. These produce correctly computed standard errors in the presence of heteroscedasticity; however, they do not correct for the actual model misspecification, so they may be more of a fig leaf than a real remedy.
Need to find out more about residuals and other data science terms? Check out our handy "What is..." guides or discover all things data science.
