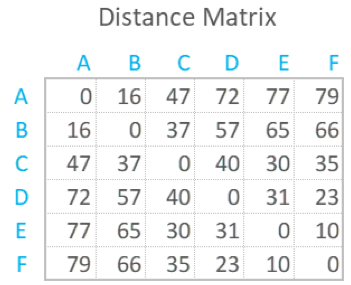
A distance matrix is a table that shows the distance between pairs of objects. For example, in the table below we can see a distance of 16 between A and B, of 47 between A and C, and so on. By definition, an object’s distance from itself, which is shown in the main diagonal of the table, is 0. Distance matrices are sometimes called dissimilarity matrices.
Applications of a distance matrix
Prior to the widespread adoption of mobile computing, the main application of a distance matrix was to show the distance between cities by road, to help with planning travel and haulage. In data analysis, distance matrices are mainly used as a data format when performing hierarchical clustering and multidimensional scaling.
How to create a distance matrix
Data can be recorded in a distance matrix at the time of collection. For example, in some studies of perception, people are asked to rate the psychological distance between pairs of objects, and these distances are recorded in a distance matrix.
More commonly, a distance matrix is computed from a raw data table. In the example below, we can use high school math (Pythagoras) to work out that the distance between A and B is
![]()
We can use the same formula with more than two variables, and this is known as the Euclidean distance.
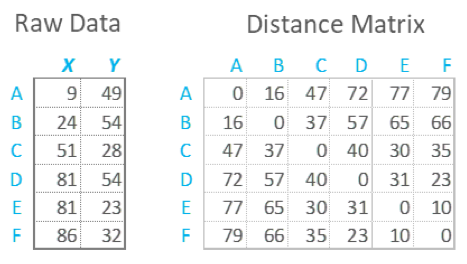
Many other ways of computing distance (distance metrics) have been developed. For example, city block distance, also known as Manhattan distance, computes the distance based on the sum of the horizontal and vertical distances (e.g., the distance between A and B is then .
A distance metric needs to be defined in a way that is sensible for the field of study. For example, if clustering crime sites in a city, city block distance may be appropriate (or, better yet, the time taken to travel between each location). Where there is no theoretical justification for an alternative, the Euclidean should generally be preferred, as it is usually an appropriate measure of distance in the physical world.
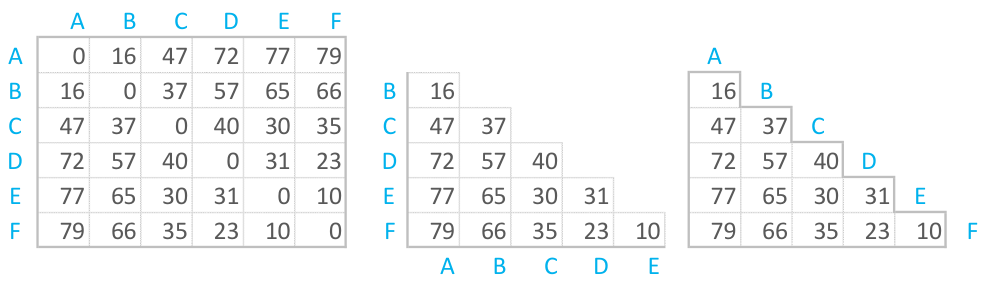
Alternative ways of displaying a distance matrix
The distance matrix shown at the beginning is the most common way of displaying distance matrices, but this is only because it is easiest way. The two other alternatives, shown below, are often better. The main diagonal, which always contains 0s and thus has no information, is removed. The upper triangular part of the matrix, which is just a mirror of the lower triangular, is also removed.
Distance matrices and dissimilarity matrices
All distance matrices are dissimilarity matrices, but not all dissimilarity matrices are distance matrices. The distances shown in a distance matrix are proportional to each other. If the distance between A and B is twice the distance between A and C, that means that B is twice as far from A as is C. By contrast, in a dissimilarity matrix the values may only reflect relative differences.