Displayr creates an online choice simulator with the click of a few buttons. In this post I describe how to create a simulator, customize both its appearance and its calculations, and provide access to the simulator for others.

Creating the simulator

  1. Create a choice model of the conjoint using hierarchical Bayes (HB), latent class analysis or Multinomial logit in Displayr (Insert > More > Conjoint/Choice Modeling). You can also do this in Q and upload the QPack to Displayr.
  2. Click on the model and in the object inspector, click Inputs > SIMULATOR > Create simulator.
  3. Indicate the number of alternatives you want to have (excluding 'none of these' alternatives) and press OK.
  4. Indicate whether you want to include Alternative as an attribute in you model. Typically you won't want to do this, as this attribute is used for model checking purposes rather than simulation.

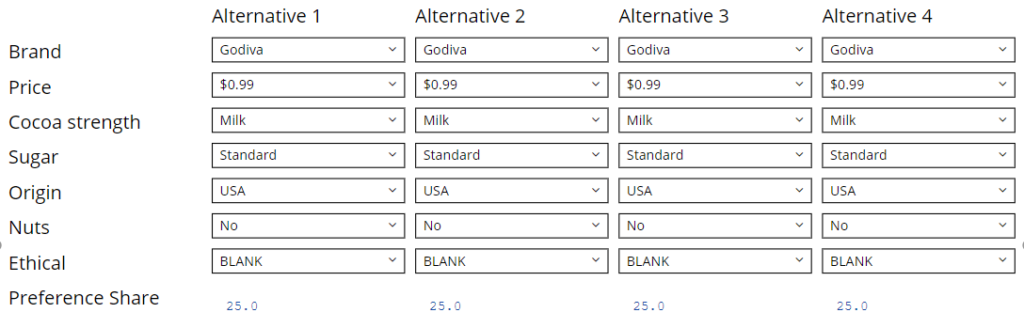
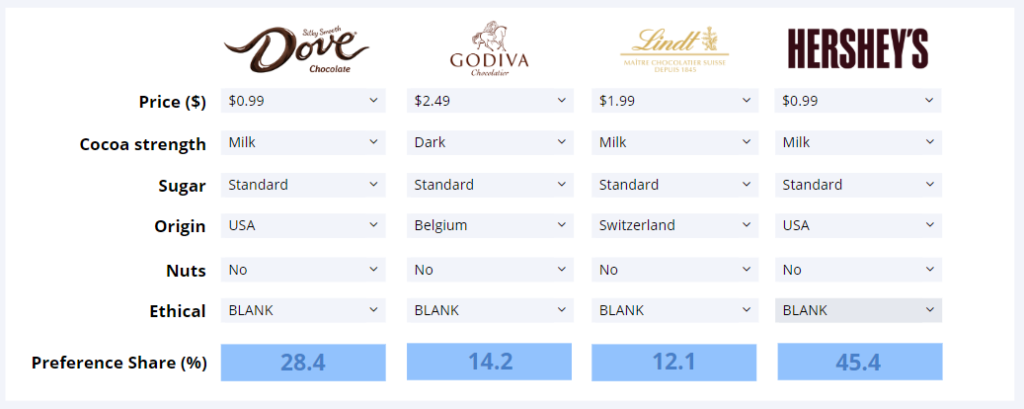
A new page will then appear beneath the page that contains your model, and this page will contain your simulator. For example, one created for on the chocolate market looks like this:

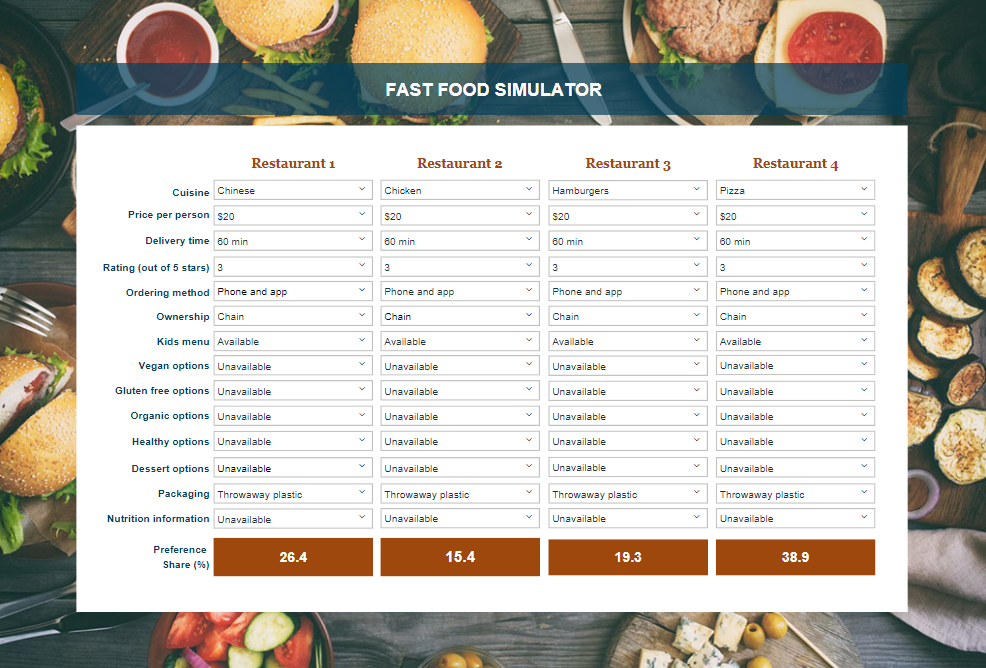
Customizing the appearance of the simulator

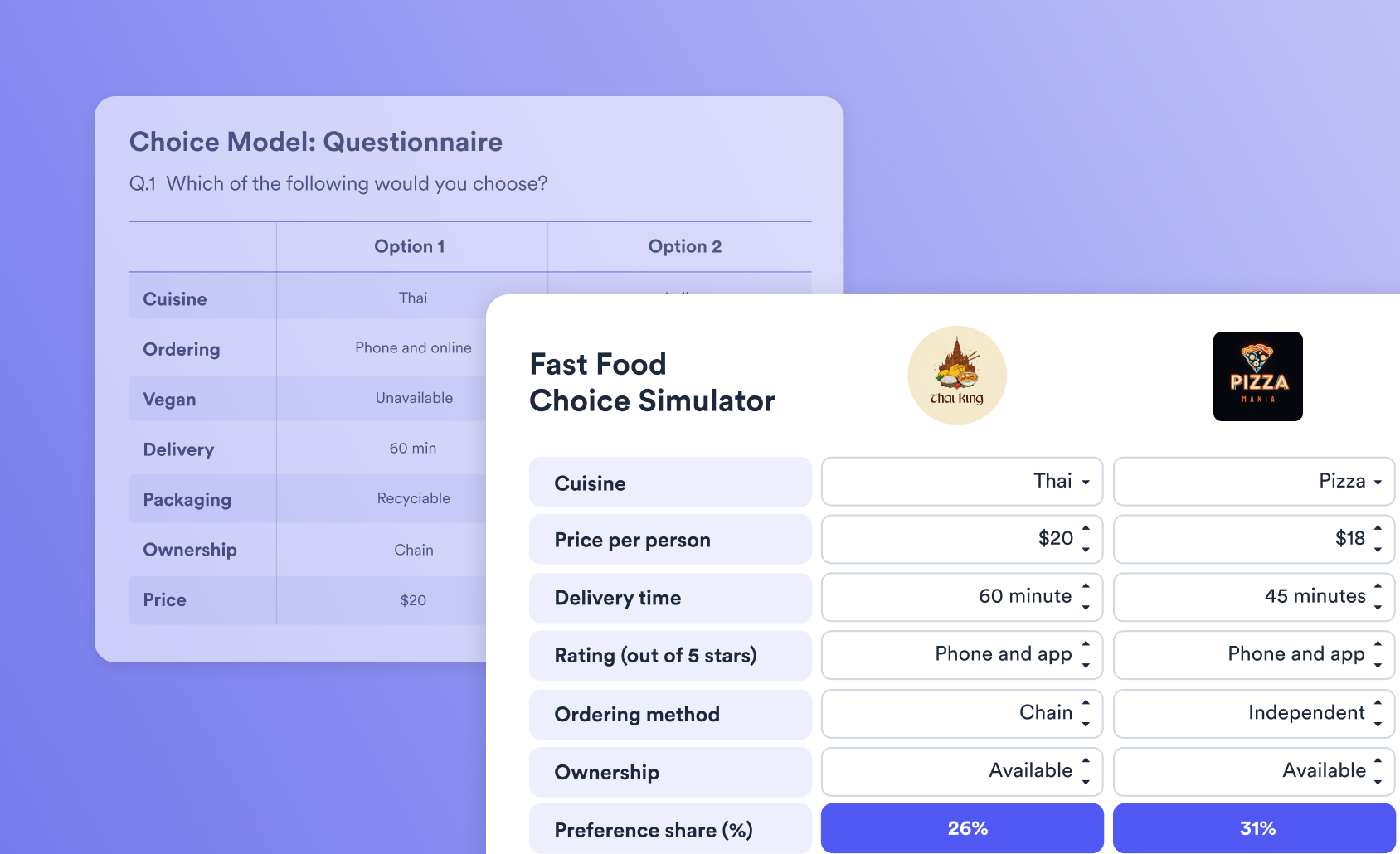
You can customize all the various components of the simulator by clicking on them to modify them. For example, we've restyled the simulator above into the more attractive simulator below. For another example, click here.

Customizing the calculations of the simulator

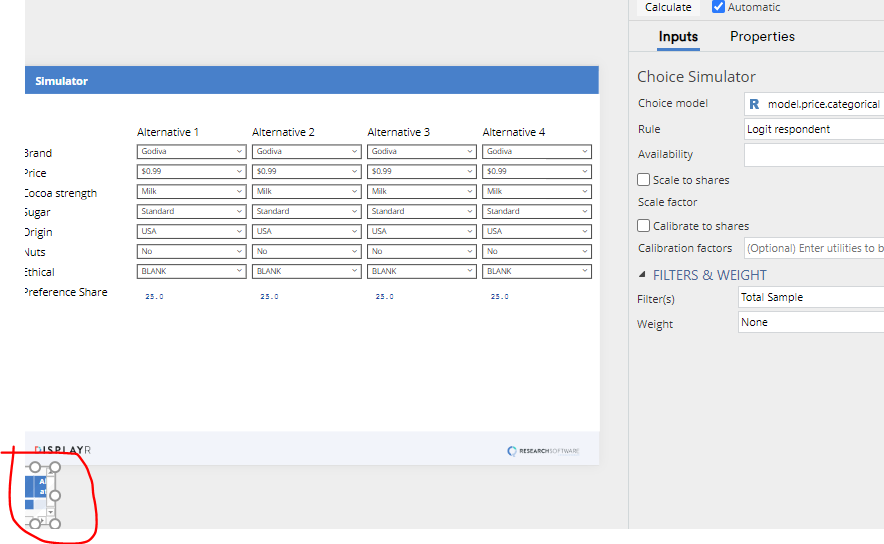
If you scroll down, you will find that below the simulator is a small table showing the simulated shares. If you click on the this table, additional options for customizing the simulator appear on the right of the screen in the object inspector. You can use these controls to:

Numeric attributes

If attributes have been analyzed as numeric (see Numeric Attributes in Choice-Based Conjoint Analysis in Displayr), when the simulator is created the combo box for the attribute will show the minimum value of the attribute used in the research, the maximum value, and two equally-spaced points in-between. For example, if the research has tested prices of $0.99 and  $2.49, the combo box will contain options of 0.99, 1.36, 1.74, 2.49.

This list of values can be edited by clicking on the combo box, and changing the values in Properties > Item list, in the object inspector. You can change the values and add additional values. The values used in the combo box are not constrained to match those used in the study. After changing the list, make sure you click on the calculations (see the image above) and press CALCULATE in the object inspector to inform the simulator of the changes.

Providing access to the simulator for others

Once you have set up a simulator in Displayr, you can publish it as a web page (Export > Web page), choosing whether to allow it to be accessed by anybody with the URL, or, setting up password access.