What is a ROC Curve and How to Interpret It

A Receiver Operator Characteristic (ROC) curve is a graphical plot used to show the diagnostic ability of binary classifiers. It was first used in signal detection theory but is now used in many other areas such as medicine, radiology, natural hazards and machine learning. In this post I'll show you how a ROC curve is created and how to interpret the ROC curve. 

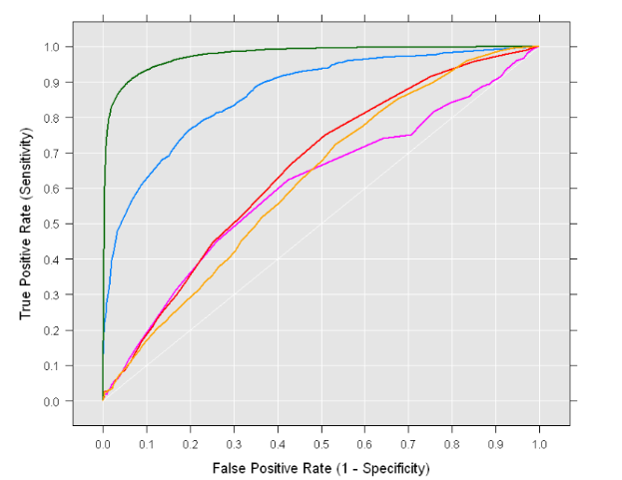
An example is shown below:

Create your own ROC curve

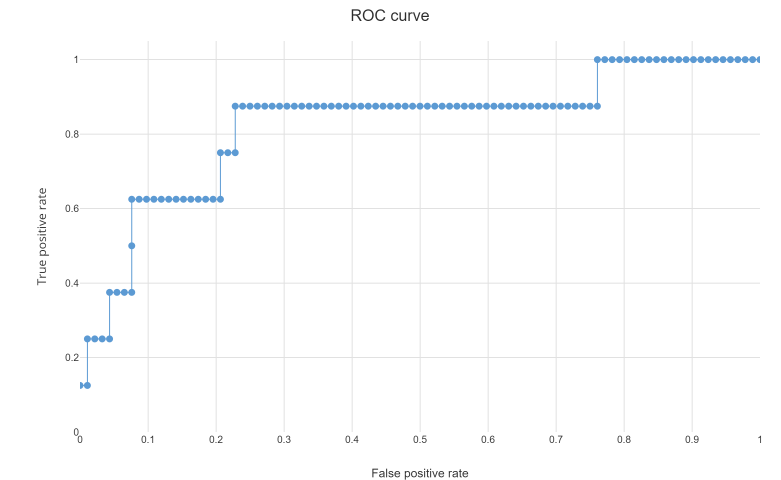
Creating a ROC curve

A ROC curve is constructed by plotting the true positive rate (TPR) against the false positive rate (FPR). The true positive rate is the proportion of observations that were correctly predicted to be positive out of all positive observations (TP/(TP + FN)). Similarly, the false positive rate is the proportion of observations that are incorrectly predicted to be positive out of all negative observations (FP/(TN + FP)). For example, in medical testing, the true positive rate is the rate in which people are correctly identified to test positive for the disease in question.

A discrete classifier that returns only the predicted class gives a single point on the ROC space. But for probabilistic classifiers, which give a probability or score that reflects the degree to which an instance belongs to one class rather than another, we can create a curve by varying the threshold for the score. Note that many discrete classifiers can be converted to a scoring classifier by ‘looking inside’ their instance statistics. For example, a decision tree determines the class of a leaf node from the proportion of instances at the node.

Create your own ROC curve

Interpreting the ROC curve

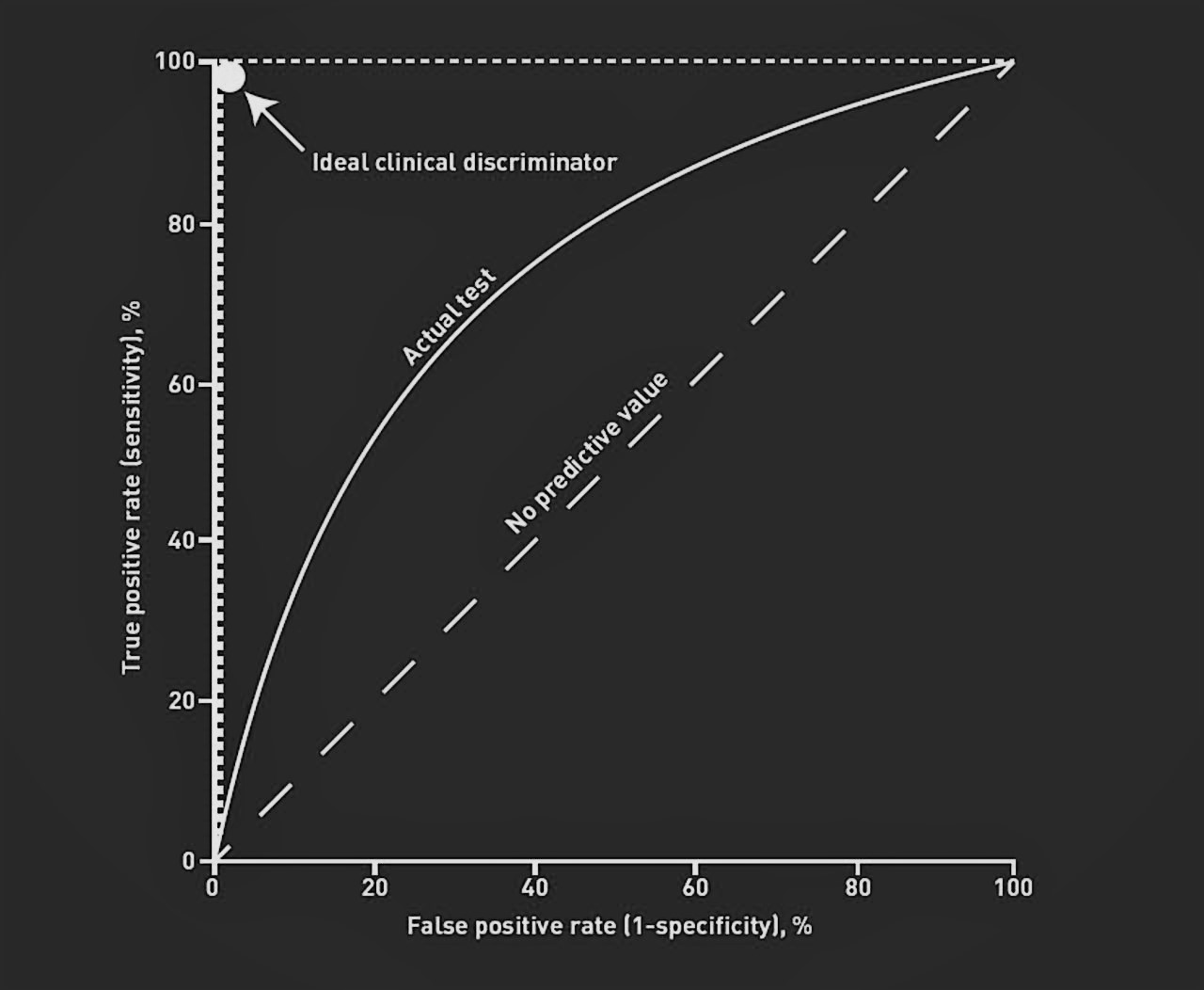
The ROC curve shows the trade-off between sensitivity (or TPR) and specificity (1 – FPR). Classifiers that give curves closer to the top-left corner indicate a better performance. As a baseline, a random classifier is expected to give points lying along the diagonal (FPR = TPR). The closer the curve comes to the 45-degree diagonal of the ROC space, the less accurate the test.

Note that the ROC does not depend on the class distribution. This makes it useful for evaluating classifiers predicting rare events such as diseases or disasters. In contrast, evaluating performance using accuracy (TP +

TN)/(TP + TN + FN + FP) would favor classifiers that always predict a negative outcome for rare events.

Create your own ROC curve

Area under curve (AUC)

To compare different classifiers, it can be useful to summarize the performance of each classifier into a single measure. One common approach is to calculate the area under the ROC curve, which is abbreviated to AUC. It is equivalent to the probability that a randomly chosen positive instance is ranked higher than a randomly chosen negative instance, i.e. it is equivalent to the two sample Wilcoxon rank-sum statistic.

A classifier with high AUC can occassionally score worse in a specific region than another classifier with lower AUC. But in practice, the AUC performs well as a general measure of predictive accuracy.