A correlation matrix is a table showing correlation coefficients between variables. Each cell in the table shows the correlation between two variables. A correlation matrix is used to summarize data, as an input into a more advanced analysis, and as a diagnostic for advanced analyses.
Key decisions to be made when creating a correlation matrix include: choice of correlation statistic, coding of the variables, treatment of missing data, and presentation.
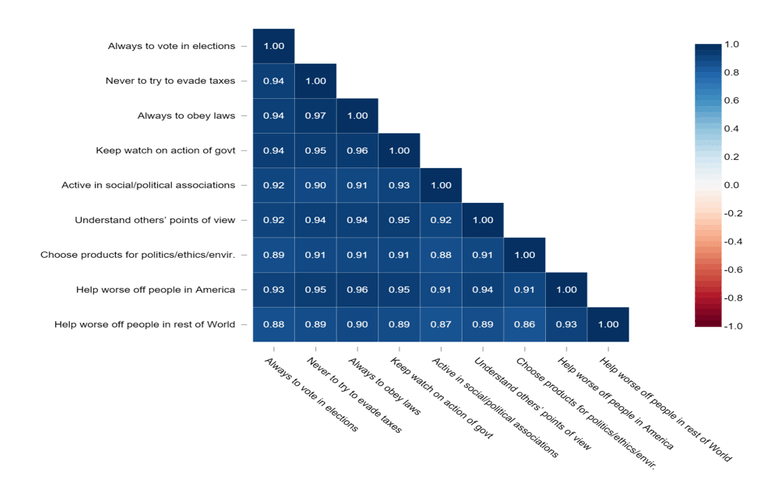
An example of a correlation matrix
Typically, a correlation matrix is “square”, with the same variables shown in the rows and columns. I've shown an example below. This shows correlations between the stated importance of various things to people. The line of 1.00s going from the top left to the bottom right is the main diagonal, which shows that each variable always perfectly correlates with itself. This matrix is symmetrical, with the same correlation is shown above the main diagonal being a mirror image of those below the main diagonal.
Create your own correlation matrix
Applications of a correlation matrix
There are three broad reasons for computing a correlation matrix:
- To summarize a large amount of data where the goal is to see patterns. In our example above, the observable pattern is that all the variables highly correlate with each other.
- To input into other analyses. For example, people commonly use correlation matrixes as inputs for exploratory factor analysis, confirmatory factor analysis, structural equation models, and linear regression when excluding missing values pairwise.
- As a diagnostic when checking other analyses. For example, with linear regression, a high amount of correlations suggests that the linear regression estimates will be unreliable.
Create your own correlation matrix
Correlation statistic
Most correlation matrixes use Pearson’s Product-Moment Correlation (r). It is also common to use Spearman’s Correlation and Kendall’s Tau-b. Both of these are non-parametric correlations and less susceptible to outliers than r.
Coding of the variables
If you also have data from a survey, you'll need to decide how to code the data before computing the correlations. For example, if respondents were given choices of Strongly Disagree, Somewhat Disagree, Neither Agree nor Disagree, Somewhat Agree, and Strongly Agree, you could assign codes of 1, 2, 3, 4, and 5, respectively (or, mathematically equivalent from the perspective of correlation, scores of -2, -1, 0, 1, and 2). However, other codings are possible, such as -4, -1, 0, 1, 4. Changes in codings tend to have little effect, except when extreme.
Treatment of missing values
The data that we use to compute correlations often contain missing values. This can either be because we did not collect this data or don’t know the responses. Various strategies exist for dealing with missing values when computing correlation matrixes. A best practice is usually to use multiple imputation.
However, people more commonly use pairwise missing values (sometimes known as partial correlations). This involves computing correlation using all the non-missing data for the two variables. Alternatively, some use listwise deletion, also known as case-wise deletion, which only uses observations with no missing data. Both pairwise and case-wise deletion assume that data is missing completely at random. This is why multiple imputation is generally the preferable option.
Create your own correlation matrix
Presentation
When presenting a correlation matrix, you'll need to consider various options including:
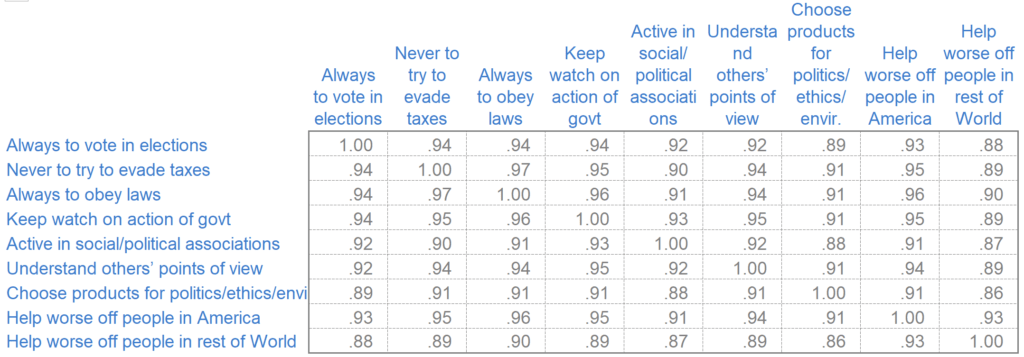
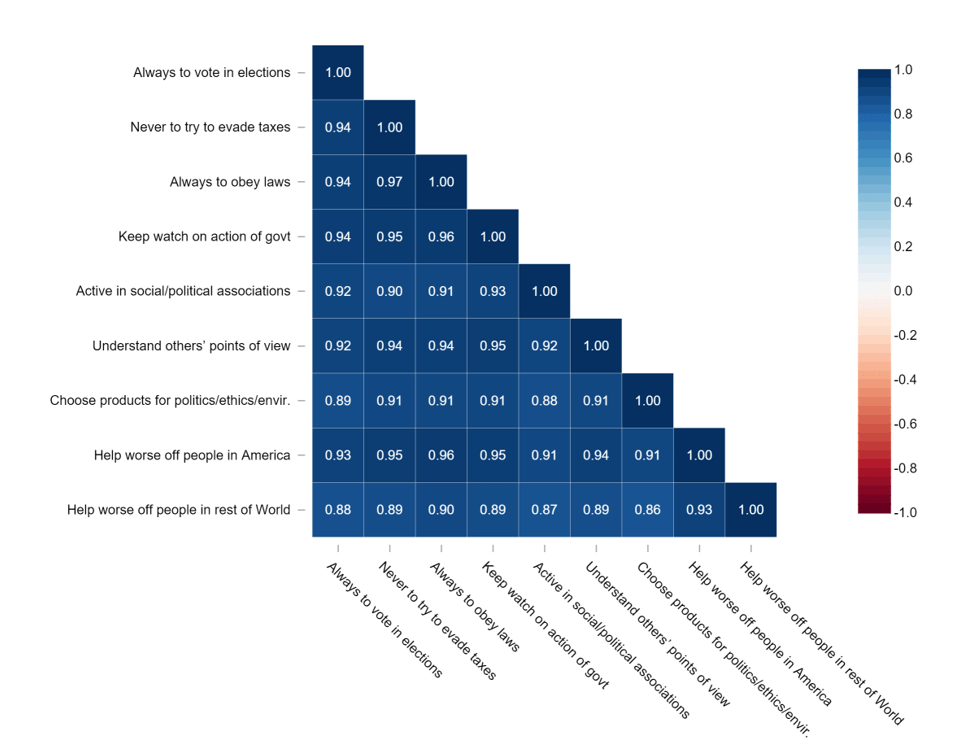
- Whether to show the whole matrix, as above or just the non-redundant bits, as below (arguably the 1.00 values in the main diagonal should also be removed).
- How to format the numbers (for example, best practice is to remove the 0s prior to the decimal places and decimal-align the numbers, as above, but this can be difficult to do in most software).
- Whether to show statistical significance (e.g., by color-coding cells red).
- Whether to color-code the values according to the correlation statistics (as shown below).
- Rearranging the rows and columns to make patterns clearer.
Want to easily create your own correlation matrix? Learn how!
Begin quickly creating your own correlation matrices in Displayr today.
